[ad_1]
Phương pháp xét tính đơn điệu dựa vào bảng biến thiên và đồ thị gồm 3 dạng: Xét tính đơn điệu dựa vào bảng biến thiên; Xét tính đơn điệu dựa vào đồ thị hàm số $y = f(x)$; Xét tính đơn điệu dựa vào đồ thị hàm số $y = f'(x)$.
I. Xét tính đơn điệu dựa vào bảng biến thiên
1. Phương pháp:
– Nếu $y’ > 0$ trên $\left( {a;b} \right)$ thì hàm số đồng biến trên $\left( {a;b} \right)$.
– Nếu $y’ < 0$ trên $\left( {a;b} \right)$ thì hàm số nghịch biến trên $\left( {a;b} \right)$.
2. Các ví dụ minh họa
Ví dụ 1. Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
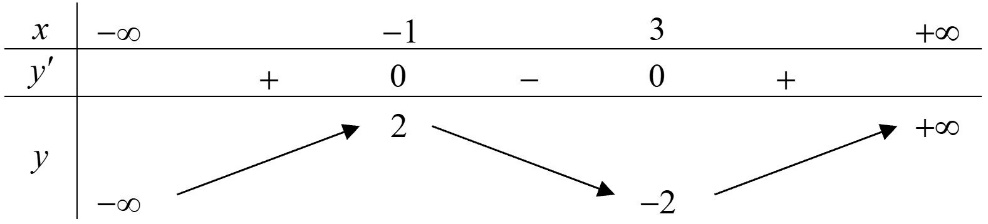
Tìm các khoảng đồng biến, nghịch biến của hàm số.
Lời giải
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên các khoảng $\left( { – \infty ; – 1} \right)$ và $\left( {3; + \infty } \right)$, nghịch biến trên khoảng $\left( { – 1;3} \right)$.
Ví dụ 2. Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
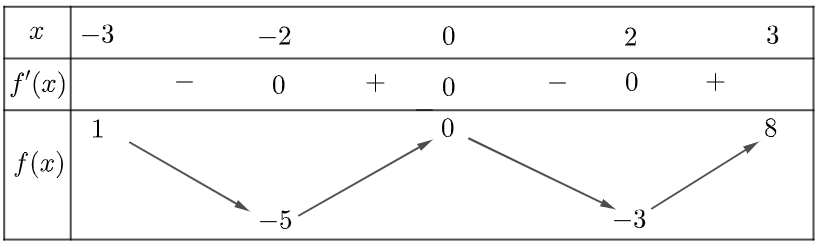
Tìm các khoảng đồng biến, nghịch biến của hàm số.
Lời giải
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên các khoảng $\left( { – 2;0} \right)$ và $\left( {2;3} \right)$, nghịch biến trên các khoảng $\left( { – 3; – 2} \right)$và $\left( {0;2} \right)$.
Ví dụ 3. Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
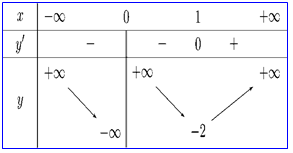
Tìm các khoảng đồng biến, nghịch biến của hàm số.
Lời giải
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng $\left( {1; + \infty } \right)$, nghịch biến trên các khoảng $\left( { – \infty ;0} \right)$ và $\left( {0;1} \right)$.
Ví dụ 4. Cho hàm số $y = f\left( x \right)$ xác định và liên tục trên $\mathbb{R}$ và có bảng biến thiên
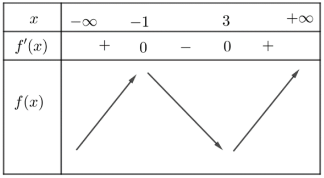
Tìm các khoảng đồng biến của hàm số $y = f\left( {2x + 1} \right)$
Lời giải
Chú ý: ${\left[ {f(u)} \right]^\prime } = u’.f'(u)$
Đặt $g\left( x \right) = f\left( {2x + 1} \right)$. Ta có $g’\left( x \right) = 2 \cdot f’\left( {2x + 1} \right)$
$g’\left( x \right) = 0 \Leftrightarrow f’\left( {2x + 1} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{2x + 1 = – 1} \\
{2x + 1 = 3}
\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – 1} \\
{x = 1}
\end{array}} \right.} \right.$
Bảng biến thiên
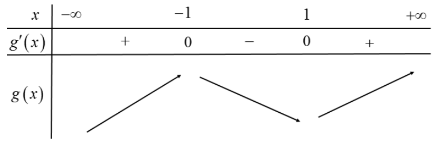
Vậy hàm số $y = f\left( {2x + 1} \right)$ đồng biến trên các khoảng $\left( { – \infty ; – 1} \right)$ và $\left( {1; + \infty } \right)$.
II. Xét tính đơn điệu dựa vào đồ thị hàm số $y = f(x)$
1. Phương pháp
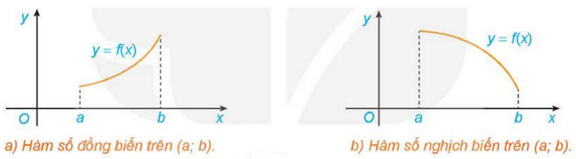
– Nếu đồ thị hàm số “đi lên” từ trái sang phải trên khoảng (a;b) thì hàm số đồng biến trên khoảng (a;b). (H.1.3a).
+ Nếu đồ thị hàm số “đi xuống” từ trái sang phải trên khoảng (a;b) thì hàm số nghịch biến trên khoảng (a;b). (H.1.3b).
2. Các ví dụ minh họa
Ví dụ 1. Cho hàm số $y = f\left( x \right)$ có đồ thị như hình vẽ bên. Tìm các khoảng đồng biến, nghịch biến của hàm số $y = f(x)$.

Lời giải
Dựa vào đồ thị hàm số $y = f\left( x \right)$ ta thấy
– Hàm số đồng biến trên các khoảng $\left( { – \infty ;0} \right)$ và $\left( {2; + \infty } \right)$.
– Hàm số nghịch biến trên khoảng $\left( {0;2} \right)$.
Ví dụ 2. Cho hàm số $y = f\left( x \right)$ có đồ thị như hình vẽ bên.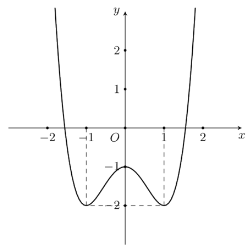
a) Từ đồ thị hàm số trên hãy vẽ bảng biến thiên
b) Tìm các khoảng đồng biến và nghịch biến.
Lời giải
a) Bảng biến thiên
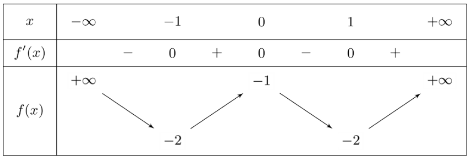
b) Hàm số đồng biến $\left( { – 1;0} \right)$ và $\left( {1; + \infty } \right)$.
Hàm số nghịch biến $\left( { – \infty ; – 1} \right)$ và $\left( {0;1} \right)$.
III. Xét tính đơn điệu dựa vào đồ thị hàm số $y = f'(x)$
1. Phương pháp
+ Nếu trên $(a;b)$ đồ thị hàm số $y = f'(x)$ nằm phía trên trục hoành thì $f'(x) > 0$ nên hàm số $y = f(x)$ đồng biến trên khoảng $(a;b)$.
+ Nếu trên $(a;b)$ đồ thị hàm số $y = f'(x)$ nằm phía dưới trục hoành thì $f'(x) < 0$ nên hàm số $y = f(x)$ nghịch biến trên khoảng $(a;b)$.
+ Nếu đồ thị hàm số $y = f'(x)$ cắt trục hoành tại điểm ${x_0}$ thì $f'({x_0}) = 0$.
2. Các ví dụ minh họa
Ví dụ 1. Cho hàm số $y = f’\left( x \right)$ có đồ thị như hình vẽ bên. Tìm các khoảng đồng biến, nghịch biến của hàm số.
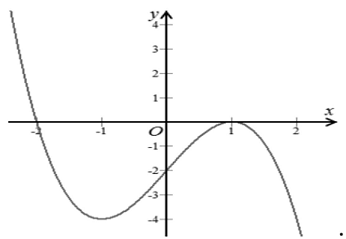
Lời giải
Trên $\left( { – \infty ; – 2} \right)$ ta thấy đồ thị $y = f’\left( x \right)$ nằm trên trục hoành nên $f’\left( x \right) > 0$ với mọi $x \in \left( { – \infty ; – 2} \right)$ nên hàm số đồng biến trên $\left( { – \infty ; – 2} \right)$.
Trên $\left( { – 2; + \infty } \right)$ ta thấy đồ thị $y = f’\left( x \right)$ nằm trên trục hoành nên $f’\left( x \right) < 0$ với mọi $x \in \left( { – 2; + \infty } \right)$ nên hàm số nghịch biến trên $\left( { – 2; + \infty } \right)$.
Ví dụ 2. Cho hàm số $y = f’\left( x \right)$ có đồ thị như hình vẽ. Tìm các khoảng đồng biến, nghịch biến của hàm số $y = f(x)$.
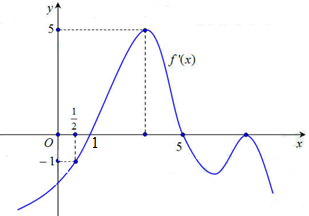
Lời giải
Dựa vào đồ thị hàm số $y = f’\left( x \right)$ ta thấy
– Hàm số đồng biến trên khoảng $\left( {1;5} \right)$.
– Hàm số nghịch biến trên các khoảng $\left( { – \infty ;1} \right)$ và $\left( {5; + \infty } \right)$.
———-
[ad_2]
PBN WEB EDU MMO TD