[ad_1]
Phương pháp:
* Đường thẳng $x = {x_0}$ được gọi là đường tiệm cận đứng của đồ thị hàm số $y = f(x)$ nếu ít nhất một trong các điều kiện sau đây thỏa mãn:
$\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty $; $\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = – \infty $; $\mathop {\lim }\limits_{x \to {x_0}^ – } f(x) = + \infty $; $\mathop {\lim }\limits_{x \to {x_0}^ – } f(x) = – \infty $.
* Đường thẳng $y = {y_0}$ được gọi là đường tiệm cận ngang của đồ thị hàm số $y = f(x)$ nếu $\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}$ hoặc $\mathop {\lim }\limits_{x \to – \infty } f(x) = {y_0}$.
* Đường thẳng $y = ax + b$ $(a \ne 0)$ gọi là đường tiệm cận xiên của đồ thị hàm số $y = f(x)$ nếu $\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) – (ax + b)} \right] = 0$ hoặc $\mathop {\lim }\limits_{x \to – \infty } \left[ {f(x) – (ax + b)} \right] = 0$
Câu 1. Tìm các tiệm cận đứng và tiệm cận ngang của đồ thị hàm số sau:
a) $y = \frac{{4x – 5}}{{2x – 3}}$
b) $y = \frac{{ – 2x + 7}}{{4x – 3}}$
c) $y = \frac{{5x}}{{3x – 7}}$.
Lời giải
a) $y = \frac{{4x – 5}}{{2x – 3}}$
Tập xác định: $D = \mathbb{R}\backslash \left\{ {\frac{3}{2}} \right\}$
* $\mathop {\lim }\limits_{x \to {{\left( {\frac{3}{2}} \right)}^ + }} y = – \infty $; $\mathop {\lim }\limits_{x \to {{\left( {\frac{3}{2}} \right)}^ – }} y = + \infty $
$ \Rightarrow $ Tiệm cận đứng của đồ thị hàm số là $x = \frac{3}{2}$.
* $\mathop {\lim }\limits_{x \to + \infty } y = \frac{4}{2} = 2$; $\mathop {\lim }\limits_{x \to – \infty } y = \frac{4}{2} = 2$
$ \Rightarrow $ Tiệm cận ngang của đồ thị hàm số là $y = 2$.
b) $y = \frac{{ – 2x + 7}}{{4x – 3}}$
Tập xác định: $D = \mathbb{R}\backslash \left\{ {\frac{3}{4}} \right\}$
* $\mathop {\lim }\limits_{x \to {{\left( {\frac{3}{4}} \right)}^ + }} y = + \infty $; $\mathop {\lim }\limits_{x \to {{\left( {\frac{3}{4}} \right)}^ – }} y = – \infty $
$ \Rightarrow $ Tiệm cận đứng của đồ thị hàm số là $x = \frac{3}{4}$.
* $\mathop {\lim }\limits_{x \to + \infty } y = \frac{{ – 2}}{4} = – \frac{1}{2}$; $\mathop {\lim }\limits_{x \to – \infty } y = \frac{{ – 2}}{4} = – \frac{1}{2}$
$ \Rightarrow $ Tiệm cận ngang của đồ thị hàm số là $y = – \frac{1}{2}$.
c) $y = \frac{{5x}}{{3x – 7}}$.
Tập xác định: $D = \mathbb{R}\backslash \left\{ {\frac{7}{3}} \right\}$
* $\mathop {\lim }\limits_{x \to {{\left( {\frac{7}{3}} \right)}^ + }} y = + \infty $; $\mathop {\lim }\limits_{x \to {{\left( {\frac{7}{3}} \right)}^ – }} y = – \infty $
$ \Rightarrow $ Tiệm cận đứng của đồ thị hàm số là $x = \frac{7}{3}$.
* $\mathop {\lim }\limits_{x \to + \infty } y = \frac{5}{3}$; $\mathop {\lim }\limits_{x \to – \infty } y = \frac{5}{3}$
$ \Rightarrow $ Tiệm cận ngang của đồ thị hàm số là $y = \frac{5}{3}$.
Câu 2. Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số sau:
a) $y = \frac{{{x^2} + 2}}{{2x – 4}}$
b) $y = \frac{{2{x^2} – 3x – 6}}{{x + 2}}$
c) $y = \frac{{2{x^2} + 9x + 11}}{{2x + 5}}$.
Lời giải
a) $y = \frac{{{x^2} + 2}}{{2x – 4}} = \frac{1}{2}x + 1 + \frac{6}{{2x – 4}}$
Tập xác định: $D = \mathbb{R}\backslash \left\{ 2 \right\}$
* $\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty $; $\mathop {\lim }\limits_{x \to {2^ – }} y = – \infty $
$ \Rightarrow $ Tiệm cận đứng của đồ thị hàm số là $x = 2$.
* $\mathop {\lim }\limits_{x \to + \infty } \left[ {y – \left( {\frac{1}{2}x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{6}{{2x – 4}} = 0$; $\mathop {\lim }\limits_{x \to – \infty } \left[ {y – \left( {\frac{1}{2}x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to – \infty } \frac{6}{{2x – 4}} = 0$
$ \Rightarrow $ Tiệm cận xiên của đồ thị hàm số là $y = \frac{1}{2}x + 1$.
b) $y = \frac{{2{x^2} – 3x – 6}}{{x + 2}} = 2x – 7 + \frac{8}{{x + 2}}$
Tập xác định: $D = \mathbb{R}\backslash \left\{ { – 2} \right\}$
* $\mathop {\lim }\limits_{x \to – {2^ + }} y = + \infty $; $\mathop {\lim }\limits_{x \to – {2^ – }} y = – \infty $
$ \Rightarrow $ Tiệm cận đứng của đồ thị hàm số là $x = – 2$.
* $\mathop {\lim }\limits_{x \to + \infty } \left[ {y – \left( {2x – 7} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{8}{{x + 2}} = 0$; $\mathop {\lim }\limits_{x \to – \infty } \left[ {y – \left( {2x – 7} \right)} \right] = \mathop {\lim }\limits_{x \to – \infty } \frac{8}{{x + 2}} = 0$
$ \Rightarrow $ Tiệm cận xiên của đồ thị hàm số là $y = 2x – 7$.
c) $y = \frac{{2{x^2} + 9x + 11}}{{2x + 5}} = x + 2 + \frac{1}{{2x + 5}}$.
Tập xác định: $D = \mathbb{R}\backslash \left\{ { – \frac{5}{2}} \right\}$
* $\mathop {\lim }\limits_{x \to {{\left( { – \frac{5}{2}} \right)}^ + }} y = + \infty $; $\mathop {\lim }\limits_{x \to {{\left( { – \frac{5}{2}} \right)}^ – }} y = – \infty $
$ \Rightarrow $ Tiệm cận đứng của đồ thị hàm số là $x = – \frac{5}{2}$.
* $\mathop {\lim }\limits_{x \to + \infty } \left[ {y – \left( {x + 2} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{2x + 5}} = 0$; $\mathop {\lim }\limits_{x \to – \infty } \left[ {y – \left( {x + 2} \right)} \right] = \mathop {\lim }\limits_{x \to – \infty } \frac{1}{{2x + 5}} = 0$
$ \Rightarrow $ Tiệm cận xiên của đồ thị hàm số là $y = x + 2$.
Câu 3. Tìm các tiệm cận của đồ thị hàm số sau:
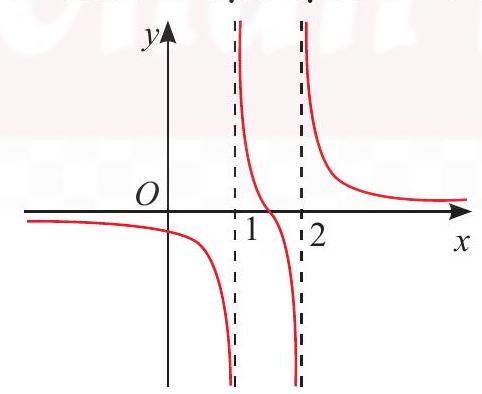
a) $y = \frac{{2x – 3}}{{5{x^2} – 15x + 10}}$
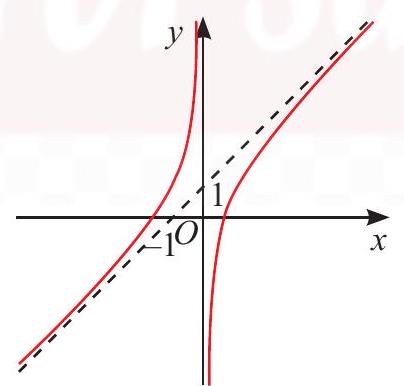
b) $y = \frac{{{x^2} + x – 1}}{x}$
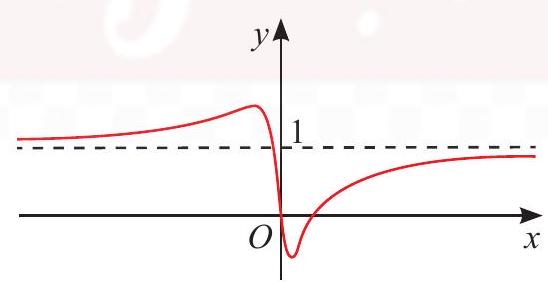
c) $y = \frac{{16{x^2} – 8x}}{{16{x^2} + 1}}$
Hình 12
Lời giải
a) $y = \frac{{2x – 3}}{{5{x^2} – 15x + 10}}$
Tập xác định: $D = \mathbb{R}\backslash \left\{ {1;2} \right\}$
* $\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty $; $\mathop {\lim }\limits_{x \to {1^ – }} y = – \infty $
$ \Rightarrow $ Tiệm cận đứng của đồ thị hàm số là $x = 1$.
* $\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty $; $\mathop {\lim }\limits_{x \to {2^ – }} y = – \infty $
$ \Rightarrow $ Tiệm cận đứng của đồ thị hàm số là $x = 2$.
* $\mathop {\lim }\limits_{x \to + \infty } y = 0$; $\mathop {\lim }\limits_{x \to – \infty } y = 0$
$ \Rightarrow $ Tiệm cận ngang của đồ thị hàm số là $y = 0$.
b) $y = \frac{{{x^2} + x – 1}}{x} = x + 1 – \frac{1}{x}$
Tập xác định: $D = \mathbb{R}\backslash \left\{ 0 \right\}$
* $\mathop {\lim }\limits_{x \to {0^ + }} y = – \infty $; $\mathop {\lim }\limits_{x \to {0^ – }} y = + \infty $
$ \Rightarrow $ Tiệm cận đứng của đồ thị hàm số là $x = 0$.
* $\mathop {\lim }\limits_{x \to + \infty } \left[ {y – \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{ – 1}}{x} = 0$; $\mathop {\lim }\limits_{x \to – \infty } \left[ {y – \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to – \infty } \frac{{ – 1}}{x} = 0$
$ \Rightarrow $ Tiệm cận xiên của đồ thị hàm số là $y = x + 1$.
c) $y = \frac{{16{x^2} – 8x}}{{16{x^2} + 1}}$
Tập xác định: $D = \mathbb{R}$
* $\mathop {\lim }\limits_{x \to + \infty } y = \frac{{16}}{{16}} = 1$; $\mathop {\lim }\limits_{x \to – \infty } y = \frac{{16}}{{16}} = 1$
$ \Rightarrow $ Tiệm cận ngang của đồ thị hàm số là $y = 1$.
Câu 4. Nồng độ oxygen trong hồ theo thời gian $t$ cho bởi công thức $y\left( t \right) = 5 – \frac{{15t}}{{9{t^2} + 1}}$, với $y$ được tính theo $mg/l$ và $t$ được tính theo giờ, $t \geqslant 0$. Tìm các đường tiệm cận của đồ thị hàm số $y\left( t \right)$. Từ đó, có nhận xét gì về nồng độ oxygen trong hồ khi thời gian $t$ trở nên rất lớn?
(Theo: www.researchgate.net/publication/264903978_Microrespirometric_ characterization_of_activated_sludge_inhibition_by_copper_and_zinc)
Lời giải
$y\left( t \right) = 5 – \frac{{15t}}{{9{t^2} + 1}}$
$\mathop {\lim }\limits_{t \to + \infty } \left[ {5 – \frac{{15t}}{{9{t^2} + 1}}} \right] = \mathop {\lim }\limits_{t \to + \infty } \frac{{45{t^2} – 15t + 5}}{{9{t^2} + 1}} = \frac{{45}}{9} = 5$
$ \Rightarrow $ Tiệm cận ngang của đồ thị hàm số là $y = 5$.
Nhận xét: Khi thời gian $t$ trở nên rất lớn thì nồng độ oxygen trong hồ gần bằng ${\text{5}}\,{\text{mg}}/l$ hay nói cách khác thời gian càng lớn thì nồng độ oxygen trong hồ ổn định gần bằng ${\text{5}}\,{\text{mg}}/l$
Câu 5. Tìm tiệm cận của đồ thị hàm số khối lượng hạt $m\left( v \right) = \frac{{{m_0}}}{{\sqrt {1 – \frac{{{v^2}}}{{{c^2}}}} }}$ trong![]() (trang 19).
(trang 19).
Lời giải
* $\mathop {\lim }\limits_{v \to {c^ + }} m(v) = + \infty $; $\mathop {\lim }\limits_{v \to {c^ – }} m(v) = – \infty $
$ \Rightarrow $ Tiệm cận đứng của đồ thị hàm số là $v = 1$.
———-
SGK T12 CTST
[ad_2]
PBN WEB EDU MMO TD