Đề thi giữa HK2 môn Toán 12 năm 2023-2024 Trường THPT Thạnh Lộc

Câu 1:

Trong không gian Oxyz. Biết mặt cầu (S) nhận hai điểm A(4;2;0), B(-2;-4;3) làm 2 đầu đường kính. Tính tâm I bán kính R của (S)?

• A.
  I (2;-2;3),\(R\)= 9

• B.
  \(I(1; – 1;\dfrac{3}{2})\),\(R = \dfrac{9}{2}\)

• C.
  \(I(1; – 1;\dfrac{3}{2})\),\(R = 9\)

• D.
  \(I(2; – 2;3)\),\(R = \dfrac{9}{2}\)

Câu 2:
Mã câu hỏi: 467338

Tìm họ nguyên hàm của hàm số sau \(f(x) = \dfrac{{{x^2} – x + 1}}{{x – 1}}\)?

• A.
  \({x^2} + \ln |x – 1| + C.\)

• B.
  \(1 + \dfrac{1}{{{{(x – 1)}^2}}} + C.\)

• C.
  \(x + \dfrac{1}{{x – 1}} + C.\)

• D.
  \(\dfrac{{{x^2}}}{2} + \ln |x – 1| + C\)

Câu 3:
Mã câu hỏi: 467343

Biết đường thẳng \(y = x – 2\) cắt đồ thị hàm số \(y = \dfrac{{2x + 1}}{{x – 1}}\) tại 2 điểm phân biệt \(A,B\) có hoành độ lần lượt \({x_A},{x_B}\). Khi đó giá trị \({x_A} + {x_B}\) bằng?

Câu 4:
Mã câu hỏi: 467348

Một người gửi tiết kiệm số tiền 18000000 đồng với lãi suất 6,0

• A.
  23000000 đồng

• B.
  24088000 đồng

• C.
  22725000 đồng

• D.
  25533000 đồng

Câu 5:
Mã câu hỏi: 467352

Với \(a\) là số thực khác 0 tùy ý, giá trị của \({\log _4}{a^2}\) bằng?

• A.
  2\({\log _2}\left| a \right|\)

• B.
  \(\dfrac{1}{4}{\log _2}\left| a \right|\)

• C.
  \({\log _2}\left| a \right|\)

• D.
  \({\log _2}a\)

Câu 6:
Mã câu hỏi: 467356

Số nghiệm nguyên nhỏ hơn 10 của bất phương trình sau \({25^x} + {5.5^x} – 6 \ge 0\) là?

Câu 7:
Mã câu hỏi: 467359

Cho hình trụ có diện tích xung quanh bằng \(8\pi {a^2}\) và độ dài đường sinh bằng \(a\). Tính thể tích của hình trụ đã cho?

• A.
  \(16\pi {a^3}\)

• B.
  \(32\pi {a^3}\)

• C.
  \(8\pi {a^3}\)

• D.
  \(24\pi {a^3}\)

Câu 8:
Mã câu hỏi: 467364

Đường tiệm cận ngang của đồ thị hàm số sau \(y = \dfrac{{x – 3}}{\begin{array}{l}x – 1\\\end{array}}\) có phương trình là?

• A.
  \(y = – 1\)

• B.
  \(y = 1\)

• C.
  \(y = 0\)

• D.
  \(x = 1\)

Câu 9:
Mã câu hỏi: 467366

Trong không gian \(Oxyz\), viết phương trình mp \((P)\) đi qua điểm \(A(2;1; – 3)\), song song với trục \(Oz\) và vuông góc với mặt phẳng \((Q):x + y – 3z = 0\)?

• A.
  \(x + y – 3 = 0\)

• B.
  \(x – y = 0\)

• C.
  \(x – y – 1 = 0\)

• D.
  \(x – y + 1 = 0\)

Câu 10:
Mã câu hỏi: 467370

Tìm mệnh đề sai trong các mệnh đề sau?

• A.
  \(\int {2{e^x}dx = 2({e^x} + C)} \)

• B.
  \(\int {\dfrac{1}{x}dx = \ln (x) + C} \)

• C.
  \(\int {{x^3}dx = \dfrac{{{x^4} + C}}{4}} \)

• D.
  \(\int {\sin {\rm{x}}dx = C – \cos x} \)

Câu 11:
Mã câu hỏi: 467372

Trong không gian \(Oxyz\), viết phương trình mp \((P)\) đi qua điểm \(A(2;1; – 3)\), song song với trục \(Oz\) và vuông góc với mặt phẳng \((Q):x + y – 3z = 0\)?

• A.
  \(x + y – 3 = 0\)

• B.
  \(x – y = 0\)

• C.
  \(x – y – 1 = 0\)

• D.
  \(x – y + 1 = 0\)

Câu 12:
Mã câu hỏi: 467373

Cho hàm số \(y = f(x)\) liên tục trên \(\left[ {a;b} \right]\). Diện tích hình phẳng giới hạn bởi ĐTHS \(y = f(x)\), trục \(Ox\) và các đường thẳng \(x = a\),\(x = b\) là?

• A.
  \(S = \int\limits_a^b {f(x)dx} \)

• B.
  \(\left| {S = \int\limits_a^b {f(x)dx} } \right|\)

• C.
  \(S = – \int\limits_a^b {f(x)dx} \)

• D.
  \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \)

Câu 13:
Mã câu hỏi: 467375

Cho \(f(x)\),\(g(x)\) là các hàm số xác định và liên tục trên \(R\). Trong các mệnh đề sau, mệnh đề nào sai?

• A.
  \(\int {\left[ {f(x) – g(x)} \right]} dx = \int {f(x)dx – \int {g(x)dx} } \)

• B.
  \(\int {2f(x)} dx = 2\int {f(x)dx} \)

• C.
  \(\int {\left[ {f(x) + g(x)} \right]} dx = \int {f(x)dx + \int {g(x)dx} } \)

• D.
  \(\int {\left[ {f(x)g(x)} \right]} dx = \int {f(x)dx.\int {g(x)dx} } \)

Câu 14:
Mã câu hỏi: 467379

Tích phân \(I = \int\limits_0^1 {\dfrac{1}{{{x^2} – x – 2}}} dx\) có giá trị bằng?

Câu 15:
Mã câu hỏi: 467381

Trong không gian \({\rm{Ox}}yz\), cho 2 điểm \(M( – 1;5;3)\),\(N(1;3;5)\). Viết phương trình mặt phẳng trung trực \((P)\) của đoạn \(MN\)?

Câu 16:
Mã câu hỏi: 467383

Cho hàm số \(f(x)\) liên tục trên \(\left[ {a;b} \right]\). Hãy chọn khẳng định đúng?

• A.
  Hàm số luôn có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn \(\left[ {a;b} \right]\)

• B.
  Hàm số không có giá trị lớn nhất trên đoạn \(\left[ {a;b} \right]\)

• C.
  Hàm số không có giá trị nhỏ nhất trên đoạn \(\left[ {a;b} \right]\)

• D.
  Hàm số luôn có cực đại và cực tiểu trên đoạn \(\left[ {a;b} \right]\)

Câu 17:
Mã câu hỏi: 467386

Cho hàm số \(y = f(x)\) có bảng biến thiên như sau:

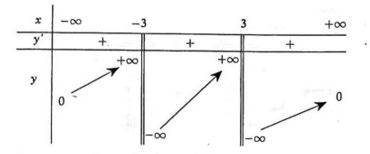
Số đường tiệm cận của đồ thị hàm số là?

Câu 18:
Mã câu hỏi: 467392

Tính diện tích \(S\) của hình phẳng \(\left( H \right)\) giới hạn bởi các đường cong \(y = – {x^3} + 12x\) và \(y = – {x^2}\)?

• A.
  \(S = \dfrac{{397}}{4}\)

• B.
  \(S = \dfrac{{343}}{{12}}\)

• C.
  \(S = \dfrac{{793}}{4}\) 

• D.
  \(S = \dfrac{{937}}{{12}}\)

Câu 19:
Mã câu hỏi: 467400

Trong không gian \({\rm{Ox}}yz\), cho tam giác\(ABC\) có trọng tâm \(G\), biết \(A\left( {1;2;0} \right)\), \(B\left( { – 4;5;3} \right)\), \(G\left( {0; – 1; – 1} \right)\). Tìm tọa độ điểm \(C\)?

Câu 20:
Mã câu hỏi: 467405

Cho 2 số thực \(a\) và \(b\) dương khác 1 với \({a^{\dfrac{4}{5}}} < {a^{\dfrac{1}{2}}}\) và \({\log _b}\dfrac{1}{3} > {\log _b}\dfrac{3}{5}\). Mệnh đề nào dưới đây đúng?

Câu 21:
Mã câu hỏi: 467409

Với giá trị nào của \(x\) thì hàm số \(f(x) = {\log _5}\left( {{x^2} – x – 2} \right)\) xác định?

• A.
  \(x \in \left( { – 1;2} \right)\)

• B.
  \(x \in \left( { – 1; + \infty } \right)\)

• C.
  \(x \in \left( { – \infty ; – 1} \right) \cup \left( {2; + \infty } \right)\)

• D.
  \(x \in \left( { – \infty ; – 1} \right] \cup \left[ {2; + \infty } \right)\)

Câu 22:
Mã câu hỏi: 467418

Cho hàm số \(f(x)\) có đạo hàm trên đoạn \(\left[ {1;3} \right]\),\(f(3) = 5\) và \(\int\limits_1^3 {f’\left( x \right)dx} = 6\). Khi đó giá trị \(f(1)\) bằng?

• A.
  1

• B.
  10      

• C.
   -1 

• D.
  11

Câu 23:
Mã câu hỏi: 467423

Diện tích hình phẳng giới hạn bởi đồ thị hàm số \((C):y = \dfrac{{ – 3x – 1}}{{x – 1}}\) và 2 trục tọa độ là \(S = 4\ln \dfrac{a}{b} – 1\) (\(a,b\) là 2 số nguyên tố cùng nhau). Tính \(a – 2b\)?

• A.
  \( – 5\) 

• B.
  \( – 2\) 

• C.
  \( – 1\) 

• D.
  1

Câu 24:
Mã câu hỏi: 467429

Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số \(y = \dfrac{1}{3}{x^3} – m{x^2} + 4x + 2\) đồng biến trên tập xác định của nó?

Câu 25:
Mã câu hỏi: 467435

Cho lăng trụ tam giác đều có tất cả các cạnh đều bằng \(\sqrt 3 \). Thể tích của khối lăng trụ đã cho bằng?

Câu 26:
Mã câu hỏi: 467440

Tập nghiệm S của bất phương trình sau \({\log _2}(5 – x) < 1\) là?

• A.
  \(S = \left( {0;2} \right)\)

• B.
  \(S = \left( {0;3} \right)\)

• C.
  \(S = \left( {3;5} \right)\)

• D.
  \(S = \left( {3; + \infty } \right)\)

Câu 27:
Mã câu hỏi: 467445

Trong không gian \({\rm{Ox}}yz\). Biết mặt cầu \((S)\) đi qua gốc tọa độ \(O\) và các điểm \(A( – 4;0;0)\), \(B(0;2;0)\), \(C\left( {0;0;4} \right)\). Phương trình \(\left( S \right)\) là?

• A.
  \({x^2} + {y^2} + {z^2} + 4x + 2y – 4z = 0\)

• B.
  \({x^2} + {y^2} + {z^2} + 4x – 2y + 4z = 0\)

• C.
  \({x^2} + {y^2} + {z^2} + 4x – 2y – 4z = 0\)

• D.
  \({x^2} + {y^2} + {z^2} + 2x – y – 2z = 0\)

Câu 28:
Mã câu hỏi: 467451

Trong không gian \({\rm{Ox}}yz\), gọi \(A,B,C\) lần lượt là hình chiếu vuông góc của điểm \(M( – 1;1;2)\) trên các trục \({\rm{Ox}},Oy,Oz\). Viết phương trình mp \((ABC)\)?

• A.
  \(2x – 2y – z = 0\)

• B.
  \(2x – 2y – z + 2 = 0\)

• C.
  \( – 2x + 2y + z + 2 = 0\)

• D.
  \(2x + 2y – z + 2 = 0\)

Câu 29:
Mã câu hỏi: 467457

Tính tích phân \(I = \int\limits_1^2 {x{e^x}dx} \) bằng?

• A.
  \(I = e\)

• B.
  \(I = 3{e^2} – 2e\)

• C.
  \(I = {e^2}\) 

• D.
  \(I =- {e^2}\)

Câu 30:
Mã câu hỏi: 467463

Trong không gian \({\rm{Ox}}yz\), tìm hình chiếu \(H\) của điểm \(A(1; – 2;3)\) trên mp \({\rm{(Ox}}y)\)?

• A.
  \(H(1; – 2;0)\) 

• B.
  \(H(1;2;0)\)

• C.
  \(H(0; – 2;3)\)

• D.
  \(H(1;0;3)\)

Câu 31:
Mã câu hỏi: 467470

Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ:

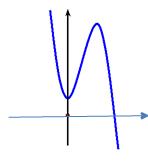
Mệnh đề nào dưới đây đúng?

• A.
  \(a < 0,b < 0,c = 0,d > 0\)

• B.
  \(a > 0,b < 0,c > 0,d > 0\)

• C.
  \(a < 0,b > 0,c = 0,d > 0\)

• D.
  \(a < 0,b > 0,c > 0,d > 0\)

Câu 32:
Mã câu hỏi: 467476

Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh 2\(a\), \(SA \bot \left( {ABC} \right)\),\(SA = a\). Thể tích của khối chóp \(S.ABC\) bằng?

• A.
  \(\dfrac{{\sqrt 3 {a^3}}}{3}\) 

• B.
  \(\sqrt 3 {a^3}\)

• C.
  \(\dfrac{{\sqrt 3 {a^3}}}{{12}}\) 

• D.
  \(\dfrac{{\sqrt 3 {a^3}}}{4}\)

Câu 33:
Mã câu hỏi: 467480

Tích phân sau \(\int\limits_0^\pi {{\rm{co}}{{\rm{s}}^2}x.{\mathop{\rm s}\nolimits} {\rm{in}}} \)\(xdx\) bằng?

• A.
  \(\dfrac{3}{2}\)

• B.
  \( – \dfrac{3}{2}\)

• C.
  \( – \dfrac{2}{3}\)

• D.
  \(\dfrac{2}{3}\)

Câu 34:
Mã câu hỏi: 467485

Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^2} – 4x + 3\), trục hoành và 2 đường thẳng \(x = 1,x = 2\) bằng?

• A.
  \(\dfrac{2}{3}\)

• B.
  \(\dfrac{3}{2}\)

   

• C.
  \(\dfrac{1}{3}\)

• D.
  \(\dfrac{7}{3}\)

Câu 35:
Mã câu hỏi: 467492

Cho hình nón bán kính đáy bằng 4. Biết rằng khi cắt hình nón đã cho bởi mặt phẳng đi qua trục ta được thiết diện là 1 tam giác đều. Diện tích xung quanh của hình nón đã cho bằng?

• A.
  \(16\pi \) 

• B.
  \(8\pi \) 

• C.
  \(12\pi \) 

• D.
  \(32\pi \)

Câu 36:
Mã câu hỏi: 467496

Gọi \(M\) và \(m\) lần lượt là GTLN và GTNN của hàm số \(y = – {x^4} + 8{x^2} – 2\) trên đoạn \(\left[ { – 3;1} \right]\). Tính \(M + m\)?

• A.
  \( – 25\) 

• B.
  \( – 6\) 

• C.
  \( – 48\) 

• D.
  \(3\)

Câu 37:
Mã câu hỏi: 467500

Giả sử \(f\) là hàm số liên tục trên khoảng \(K\) và \(a,\) \(b,\) \(c\) là 3 số bất kỳ trên khoảng \(K\). Khẳng định nào sau đây sai?

• A.
  \(\int\limits_a^c {f(x)dx + \int\limits_c^b {f(x)dx = \int\limits_a^b {f(x)dx} } } \),\(c \in \left( {a;b} \right)\)\(\) 

• B.
  \(\int\limits_a^b {f(x)dx = \int\limits_a^b {f(t)dt} } \)

• C.
  \(\int\limits_a^a {f(x)dx = 1} \) 

• D.
  \(\int\limits_a^b {f(x)dx = – \int\limits_b^a {f(x)dx} } \)

Câu 38:
Mã câu hỏi: 467506

Hàm số \(y = {x^4} – 3{x^2} + 1\) có bao nhiêu cực trị?

• A.
  một cực đại và hai cực tiểu

• B.
  một cực tiểu và cực đại

• C.
  một cực đại duy nhất 

• D.
  một cực tiểu duy nhất

Câu 39:
Mã câu hỏi: 467511

Cho đồ thị hàm số \(y = f(x)\) như hình:

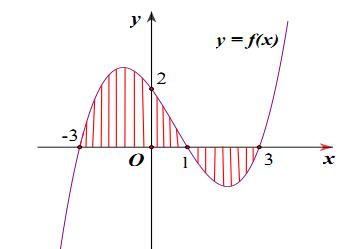
Diện tích \(S\) của hình phẳng được giới hạn bởi đồ thị hàm số \(y = f(x)\) và trục \({\rm{Ox}}\) (phần gạch sọc) được tính bởi công thức?

• A.
  \(S = \int\limits_{ – 3}^1 {f(x)dx + \int\limits_1^3 {f(x)dx} } \)

• B.
  \(S = \int\limits_{ – 3}^1 {f(x)dx – \int\limits_1^3 {f(x)dx} } \)

• C.
  \(S = \int\limits_{ – 3}^3 {f(x)dx} \)

• D.
  \(S = \left| {S = \int\limits_{ – 3}^3 {f(x)dx} } \right|\)

Câu 40:
Mã câu hỏi: 467516

Cho hình lập phương có đường chéo bằng \(2\sqrt 3 \). Thể tích mặt cầu ngoại tiếp hình lập phương đó là?

• A.
  \(12\sqrt 3 \pi \)

• B.
  \(3\sqrt 3 \pi \)

• C.
  \(\sqrt 3 \pi \)

• D.
  \(4\sqrt 3 \pi \)