[ad_1]
Câu 1. Tính:
a) $\vec a \cdot \vec b$ với $\vec a = \left( {5;2; – 4} \right),\vec b = \left( {4; – 2;2} \right)$.
b) $\vec c \cdot \vec d$ với $\vec c = \left( {2; – 3;4} \right),\vec d = \left( {6;5; – 3} \right)$.
Lời giải
Phương pháp: Cho $\overrightarrow a = \left( {{a_1};{a_2};{a_3}} \right),\,\overrightarrow b = \left( {{b_1};{b_2};{b_3}} \right)$. Ta có:
$\overrightarrow a .\overrightarrow b = {a_1}{b_1} + {a_2}{b_2} + {a_3}{b_3}$
a) $\vec a \cdot \vec b = 5 \cdot 4 + 2 \cdot \left( { – 2} \right) + 2 \cdot \left( { – 4} \right) = 8$;
b) $\vec c \cdot \vec d = 2 \cdot 6 + \left( { – 3} \right) \cdot 5 + 4 \cdot \left( { – 3} \right) = – 15$
Câu 2. Cho hai vectơ $\vec a = \left( {0;1;3} \right)$ và $\vec b = \left( { – 2;3;1} \right)$. Tìm tọa độ của vectơ $2\vec b – \frac{3}{2}\vec a$.
Lời giải
Phương pháp: Cho $\overrightarrow a = \left( {{a_1};{a_2};{a_3}} \right)$. Ta có:
$k\overrightarrow a = \left( {k{a_1};k{a_2};k{a_3}} \right)$
Ta có: $\frac{3}{2}\vec a = \left( {0;\frac{3}{2};\frac{9}{2}} \right);2\vec b = \left( { – 4;6;2} \right)$.
Toạ độ của vecto $2\vec b – \frac{3}{2}\vec a = \left( { – 4 – 0;6 – \frac{3}{2};2 – \frac{9}{2}} \right) = \left( { – 4;\frac{9}{2}; – \frac{5}{2}} \right)$
Câu 3. Cho ba điểm $A\left( {2;1; – 1} \right),B\left( {3;2;0} \right)$ và $C\left( {2; – 1;3} \right)$.
a) Chứng minh rằng $A,B,C$ là ba đỉnh của một tam giác. Tính chu vi tam giác $ABC$.
b) Tìm toạ độ trung điểm của các cạnh của tam giác $ABC$.
c) Tìm toạ độ trọng tâm $G$ của tam giác $ABC$.
Lời giải
a)
Phương pháp: Cho $\overrightarrow a = \left( {{a_1};{a_2};{a_3}} \right),\,\overrightarrow b = \left( {{b_1};{b_2};{b_3}} \right)$.
+ Nếu $\frac{{{a_1}}}{{{b_1}}} \ne \frac{{{a_2}}}{{{b_2}}}$ hoặc $\frac{{{a_2}}}{{{b_2}}} \ne \frac{{{a_3}}}{{{b_3}}}$ hoặc $\frac{{{a_3}}}{{{b_3}}} \ne \frac{{{a_1}}}{{{b_1}}}$ thì hai vectơ $\overrightarrow a $ và $\overrightarrow b $ không cùng phương.
+ Độ dài vectơ $\overrightarrow a $ là: $\left| {\overrightarrow a } \right| = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} $.
Ta có $\overrightarrow {AB} = \left( {1;1;1} \right)$; $\overrightarrow {AC} = \left( {0; – 2;4} \right)$;$\overrightarrow {BC} = \left( { – 1; – 3;3} \right)$.
Xét $\overrightarrow {AB} = \left( {1;1;1} \right)$; $\overrightarrow {AC} = \left( {0; – 2;4} \right)$, ta có $\frac{1}{{ – 2}} \ne \frac{1}{4}$
Nên $\overrightarrow {AB} $ và $\overrightarrow {AC} $ không cùng phương
Suy ra, $A,B,C$ không thẳng hàng.
Do đó $A,B,C$ là ba đỉnh của tam giác.
Ta có chu vi tam giác là:
$AB + AC + BC = \left| {\overrightarrow {AB} } \right| + \left| {\overrightarrow {AC} } \right| + \left| {\overrightarrow {BC} } \right|$
$ = \sqrt {{1^2} + {1^2} + {1^2}} + \sqrt {{0^2} + {{( – 2)}^2} + {4^2}} + \sqrt {{{( – 1)}^2} + {{( – 3)}^2} + {3^2}} $
$ = \sqrt 3 + 2\sqrt 5 + \sqrt {19} $
b)
Phương pháp: Cho $A\left( {{x_A};{y_A};{z_A}} \right)$, $B\left( {{x_B};{y_B};{z_B}} \right)$, $C\left( {{x_C};{y_C};{z_C}} \right)$. Khi đó
+ $I\left( {{x_I};{y_I};{z_I}} \right)$ là trung điểm $AB$$ \Rightarrow \left\{ \begin{gathered}
{x_I} = \frac{{{x_A} + {x_B}}}{2} \hfill \\
{y_I} = \frac{{{y_A} + {y_B}}}{2} \hfill \\
{z_I} = \frac{{{z_A} + {z_B}}}{2} \hfill \\
\end{gathered} \right.$ hay $\left\{ \begin{gathered}
{x_A} = 2{x_I} – {x_B} \hfill \\
{y_A} = 2{y_I} – {y_B} \hfill \\
{z_A} = 2{z_I} – {z_B} \hfill \\
\end{gathered} \right.$
+ $G\left( {{x_G};{y_G};{z_G}} \right)$ là trọng tâm $\Delta ABC$$ \Rightarrow \left\{ \begin{gathered}
{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} \hfill \\
{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} \hfill \\
{z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} \hfill \\
\end{gathered} \right.$
Gọi $M,N,P$ lần lượt là trung điểm của cạnh $AB,BC,CA$.
Toạ độ điểm $M$ là $M\left( {\frac{{2 + 3}}{2};\frac{{1 + 2}}{2};\frac{{ – 1 + 0}}{2}} \right)$ hay $M\left( {\frac{5}{2};\frac{3}{2}; – \frac{1}{2}} \right)$.
Toạ độ điểm $N$ là $N\left( {\frac{{2 + 3}}{2};\frac{{2 – 1}}{2};\frac{{0 + 3}}{2}} \right)$ hay $N\left( {\frac{5}{2};\frac{1}{2};\frac{3}{2}} \right)$.
Toạ độ điểm $P$ là $P\left( {\frac{{2 + 2}}{2};\frac{{1 – 1}}{2};\frac{{ – 1 + 3}}{2}} \right)$ hay $P\left( {2;0;1} \right)$.
c) Toạ độ trọng tâm $G$ của tam giác $ABC$ là $G\left( {\frac{{2 + 3 + 2}}{3};\frac{{1 + 2 – 1}}{3};\frac{{ – 1 + 0 + 3}}{3}} \right)$ hay $G\left( {\frac{7}{3};\frac{2}{3};\frac{2}{3}} \right)$.
Câu 4. Cho điểm $M\left( {1;2;3} \right)$. Hãy tìm tọa độ của các điểm:
a) ${M_1},{M_2},{M_3}$ lần lượt là hình chiếu vuông góc của $M$ trên các mặt phẳng tọa độ $\left( {Oxy} \right),\left( {Oyz} \right),\left( {Oxz} \right)$.
b) $M’,M”,M”’$ lần lượt là điểm đối xứng của $M$ qua $O$, mặt phẳng $\left( {Oxy} \right)$ và trục $Oy$.
Lời giải
Phương pháp: Cho $M\left( {{x_M};{y_M};{z_M}} \right)$. Khi đó,
+ Hình chiếu của $M$ lên $(Oxy)$ có tọa độ là: $\left( {{x_M};{y_M};0} \right)$.
+ Hình chiếu của $M$ lên $(Oyz)$ có tọa độ là: $\left( {0;{y_M};{z_M}} \right)$.
+ Hình chiếu của $M$ lên $(Oxz)$ có tọa độ là: $\left( {{x_M};0;{z_M}} \right)$
a) Ta có ${M_1}\left( {1;2;0} \right);{M_2}\left( {0;2;3} \right);{M_3}\left( {1;0;3} \right)$.
b)
* Tìm tọa độ $M’$ thỏa mãn $O$ là trung điểm của $MM’$;
Vì $O$ là trung điềm của $MM’$ nên $\left\{ {\begin{array}{*{20}{l}}
{{x_{M’}} = 2{x_O} – {x_M}} \\
{{y_{M’}} = 2{y_O} – {y_M}} \\
{{z_{M’}} = 2{z_O} – {z_M}}
\end{array}} \right.$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_{M’}} = 2.0 – 1} \\
{{y_{M’}} = 2.0 – 2} \\
{{z_{M’}} = 2.0 – 3}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_{M’}} = – 1} \\
{{y_{M’}} = – 2} \\
{{z_{M’}} = – 3}
\end{array}} \right.} \right.$.
Vậy $M’\left( { – 1; – 2; – 3} \right)$.
* Tìm tọa độ $M”$ thỏa mãn $MM”$ vuông góc và cắt mặt phẳng $\left( {Oxy} \right)$ tại điểm $H$ sao cho $H$ là trung điểm của $MM”$.
Vì $H \in \left( {Oxy} \right)$ nên $H\left( {x;y;0} \right)$. Ta có $\overrightarrow {MH} = \left( {x – 1;y – 2; – 3} \right)$.
Vì $MH \bot \left( {Oxy} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{MH \bot Ox} \\
{MH \bot Oy}
\end{array}} \right.$
$ \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {MH} .\vec i = 0} \\
{\overrightarrow {MH} \cdot \overrightarrow j = 0}
\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{x – 1 = 0} \\
{y – 2 = 0}
\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{x = 1} \\
{y = 2}
\end{array}} \right.} \right.} \right.$.
Do đó $H\left( {1;2;0} \right)$.
Vì $H$ là trung điểm của $MM”$ nên $\left\{ {\begin{array}{*{20}{l}}
{{x_{M”}} = 2{x_H} – {x_M}} \\
{{y_{M”}} = 2{y_H} – {y_M}} \\
{{z_{M”}} = 2{z_H} – {z_M}}
\end{array}} \right.$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_{M”}} = 2.1 – 1} \\
{{y_{M”}} = 2.2 – 2} \\
{{z_{M”}} = 2.0 – 3}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_{M”}} = 1} \\
{{y_{M”}} = 2} \\
{{z_{M”}} = – 3}
\end{array}} \right.} \right.$.
Vậy $M”\left( {1;2; – 3} \right)$.
* Tìm tọa độ $M”’$ thỏa mãn $MM”’$ vuông góc và cắt trục $Oy$ tại điểm $K$ sao cho $K$ là trung điểm của $MM”’$.
Vì $K \in Oy$ nên $K\left( {0;y;0} \right) \Rightarrow \overrightarrow {MK} = \left( { – 1;y – 2; – 3} \right)$.
Vì $MK \bot Oy$ nên $\overrightarrow {HK} \cdot \vec j = 0 \Leftrightarrow y – 2 = 0 \Leftrightarrow y = 2$.
Do đó $K\left( {0;2;0} \right)$.
Vì $K$ là trung điểm của $MM”’$ nên $\left\{ {\begin{array}{*{20}{l}}
{{x_{M”’}} = 2{x_K} – {x_M}} \\
{{y_{M”’}} = 2{y_K} – {y_M}} \\
{{z_{M”’}} = 2{z_K} – {z_M}}
\end{array}} \right.$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_{M”’}} = 2.0 – 1} \\
{{y_{M”’}} = 2.2 – 2} \\
{{z_{M”’}} = 2.0 – 3}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_{M”’}} = – 1} \\
{{y_{M”’}} = 2} \\
{{z_{M”’}} = – 3}
\end{array}} \right.} \right.$.
Vậy $M”’\left( { – 1;2; – 3} \right)$.
Câu 5. Cho ba điểm $A\left( {3;3;3} \right),B\left( {1;1;2} \right)$ và $C\left( {5;3;1} \right)$.
a) Tìm điểm $M$ trên trục $Oy$ cách đều hai điểm $B,C$.
b) Tìm điểm $N$ trên mặt phẳng $\left( {Oxy} \right)$ cách đều ba điểm $A,B,C$.
Lời giải
a) Vì $M \in Oy$ nên $M\left( {0;y;0} \right)$.
Vì $M$ cách đều hai điểm $B,C$ nên
$MB = MC$$ \Leftrightarrow M{B^2} = M{C^2}$
$ \Leftrightarrow {1^2} + {(1 – y)^2} + {2^2} = {5^2} + {(3 – y)^2} + {1^2}$
$ \Leftrightarrow 4y = 29 \Leftrightarrow y = \frac{{29}}{4}$.
Vậy $M\left( {0;\frac{{29}}{4};0} \right)$.
b) Vì $N \in \left( {Oxy} \right)$ nên $N\left( {x;y;0} \right)$.
Vì $N$ cách đều ba điểm $A,B,C$ nên $NA = NB = NC$
$ \Leftrightarrow N{A^2} = N{B^2} = N{C^2}$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{{(3 – x)}^2} + {{(3 – y)}^2} + {3^2} = {{(1 – x)}^2} + {{(1 – y)}^2} + {2^2}} \\
{{{(3 – x)}^2} + {{(3 – y)}^2} + {3^2} = {{(5 – x)}^2} + {{(3 – y)}^2} + {1^2}}
\end{array}} \right.$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{4x + 4y = 21} \\
{4x = 8}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{y = \frac{{13}}{4}} \\
{x = 2}
\end{array}} \right.} \right.$
Vậy $N\left( {2;\frac{{13}}{4};0} \right)$.
Câu 6. Cho các điểm $A\left( { – 1; – 1;0} \right),B\left( {0;3; – 1} \right),C\left( { – 1;14;0} \right),D\left( { – 3;6;2} \right)$.
Chứng minh rằng $ABCD$ là hình thang.
Lời giải
Ta có $\overrightarrow {AB} = \left( {1;4; – 1} \right);\overrightarrow {AC} = \left( {0;15;0} \right);\overrightarrow {DC} = \left( {2;8; – 2} \right)$.
Vì $\overrightarrow {DC} = \left( {2;8; – 2} \right) = 2\left( {1; – 4; – 1} \right) = 2\overrightarrow {AB} $ nên $\overrightarrow {DC} $ và $\overrightarrow {AB} $ cùng phương.
Mặt khác $\overrightarrow {AB} $ và $\overrightarrow {AC} $ không cùng phương nên $CD//AB$.
Do đó $ABCD$ là hình thang.
Câu 7. Cho hình hộp $ABCD.A’B’C’D’$ có $A\left( {1;0;1} \right),B\left( {2;1;2} \right)$, $D\left( {1; – 1;1} \right),C’\left( {4;5; – 5} \right)$. Tìm toạ độ các đỉnh còn lại của hình hộp.
Lời giải
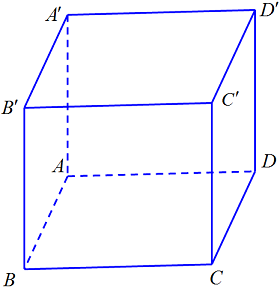
Do $ABCD \cdot A’B’C’D’$ là hình hộp nên các mặt là hình bình hành.
Ta có $\overrightarrow {AD} = \overrightarrow {BC} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{1 – 1 = {x_C} – 2} \\
{ – 1 – 0 = {y_C} – 1} \\
{1 – 1 = {z_C} – 2}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_C} = 2} \\
{{y_C} = 0} \\
{{z_C} = 2}
\end{array}} \right.} \right.$.
Vậy $C\left( {2;0;2} \right)$.
Ta có $\overline {DC} = \overrightarrow {D’C’} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{2 – 1 = 4 – {x_{D’}}} \\
{1 = 5 – {y_{D’}}} \\
{2 – 1 = – 5 – {x_{D’}}}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_{D’}} = 3} \\
{{y_{D’}} = 4} \\
{{z_{D’}} = – 6}
\end{array}} \right.} \right.$.
Vậy $D’\left( {3;4; – 6} \right)$.
Ta có $\overrightarrow {AD} = \overrightarrow {A’D’} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{1 – 1 = 3 – {x_A}} \\
{ – 1 – 0 = 4 – {y_A}} \\
{1 – 1 = – 6 – {z_A}}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_A} = 3} \\
{{y_A} = 5} \\
{{z_A} = – 6}
\end{array}} \right.} \right.$.
Vậy $A’\left( {3;5; – 6} \right)$.
Ta có $\overrightarrow {A’D’} = \overrightarrow {B’C’} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{3 – 3 = 4 – {x_{B’}}} \\
{4 – 5 = 5 – {y_{B’}}} \\
{ – 6 + 6 = – 5 – {z_{B’}}}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_{B’}} = 4} \\
{{y_{B’}} = 6} \\
{{z_{B’}} = – 5}
\end{array}} \right.} \right.$.
Vậy $B’\left( {4;6; – 5} \right)$.
Câu 8. Tính công sinh bởi lực $\vec F = \left( {20;30; – 10} \right)$ (đơn vị: $N$ ) tạo bởi một drone giao hàng (Hình 7) khi thực hiện một độ dịch chuyển $\vec d = \left( {150;200;100} \right)$ (đơn vị: $m$ ).

Hình 7
Lời giải
Công sinh bởi lực $\vec F$ là $\vec A = \vec F \cdot \vec d = 20.150 + 30 \cdot 200 + \left( { – 10} \right) \cdot 100 = 8000\;J$.
———-
[ad_2]
PBN WEB EDU MMO TD