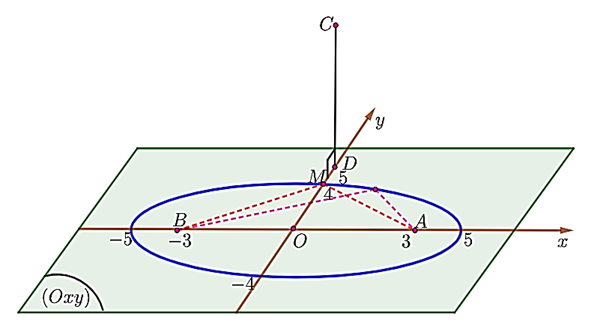
Nhận xét: Hai điểm $A,\,\,B$ cùng thuộc mặt phẳng $\left(Oxy\right)$ và $MA+MB=10>6=AB$. Do vậy, tập hợp điểm M là một elip thuộc mặt phẳng $\left(Oxy\right)$ với hai tiểu điểm là A và B.
Đặt $MA+MB=2a=10\Rightarrow a=5$, $AB=2c=6\Rightarrow c=3$, $b=\sqrt {a^{2}-c^{2}} =\sqrt {5^{2}-3^{2}} =4$.
Do vậy $M\in \left(E\right):\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ hay $M\in \left(E\right):\dfrac{x^{2}}{25}+\dfrac{y^{2}}{16}=1$.
Gọi $D\left(0;5;0\right)$là hình chiếu của $C$ trên mặt phẳng $\left(Oxy\right)$. Khi đó ta có: $CD=\sqrt{0+1^2} =1$ và $MC=\sqrt{CD^{2}+DM^{2}} =\sqrt{1+DM^{2}} \,\,\,\,\left(*\right)$.
Do vậy $MC$ bé nhất khi và chỉ khi $DM$ bé nhất.
Theo hình vẽ, ta thấy khi M trùng với đỉnh elip (E) thuộc tia Oy thì $DM$ bé nhất, hay $M\left(0;4;0\right)$.
Suy ra $DM=1$, khi đó .

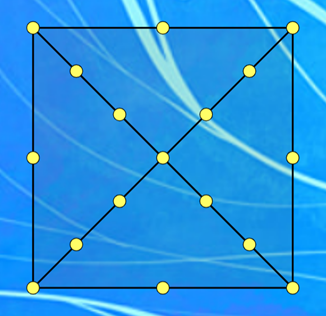
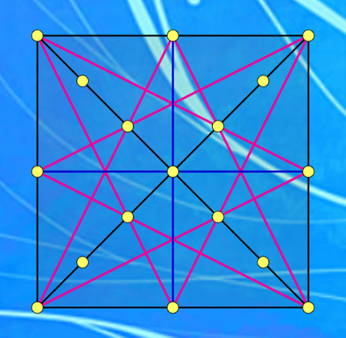 Phút thứ 3: Số phần tử không gian mẫu là $n\left(\Omega _{3}\right)=C_{17}^{3}$.
Phút thứ 3: Số phần tử không gian mẫu là $n\left(\Omega _{3}\right)=C_{17}^{3}$. Nhận xét: Hai điểm $A,\,\,B$ cùng thuộc mặt phẳng $\left(Oxy\right)$ và $MA+MB=10>6=AB$. Do vậy, tập hợp điểm M là một elip thuộc mặt phẳng $\left(Oxy\right)$ với hai tiểu điểm là A và B.
Nhận xét: Hai điểm $A,\,\,B$ cùng thuộc mặt phẳng $\left(Oxy\right)$ và $MA+MB=10>6=AB$. Do vậy, tập hợp điểm M là một elip thuộc mặt phẳng $\left(Oxy\right)$ với hai tiểu điểm là A và B.